オームの法則(V=RI)の使い方についてまとめました。
オームの法則
電気回路における電圧![]() 、電流
、電流![]() 、抵抗値
、抵抗値![]() には以下の関係が成立します。
には以下の関係が成立します。
![]()
つまり、電圧![]() 、電流
、電流![]() 、抵抗値
、抵抗値![]() のうち2つがわかれば残り1つも求めることができます。
のうち2つがわかれば残り1つも求めることができます。
- 【計算例1】
- 電気回路の抵抗Rが10[Ω]、電流が5[A]のとき、電圧V[V]はいくらか。
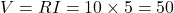 [V]
[V]
- 【計算例2】
- 電気回路の電圧が10[V]、電流が5[A]のとき、抵抗R[Ω]はいくらか。
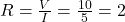 [Ω]
[Ω]
合成抵抗(直列と並列の違い)
- 抵抗
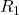 と
と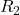 が直列に接続されているとき、合成抵抗
が直列に接続されているとき、合成抵抗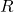 は以下の式で計算できます。
は以下の式で計算できます。
![]()
- 抵抗
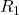 と
と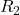 が並列に接続されているとき、合成抵抗
が並列に接続されているとき、合成抵抗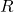 は以下の式で計算できます。
は以下の式で計算できます。
![]()
![]()
分圧の法則
直列回路において,各抵抗にかかる電圧は以下の式で計算できます。
![]()
![]()
分流の法則
並列回路において,各抵抗に流れる電流は以下の式で計算できます。
![]()
![]()
直流ブリッジの平衡条件
- 直流ブリッジ回路において、以下の式が成立するとき、電流Iが流れません。
![]()
【補足】
– これを応用し、抵抗を測定することができます。詳細は以下のページで解説しています。
–
【例題1】直流回路の端子電圧からの電源電圧の導出
【電験3種 理論 令和4年度下期 問題5 一部改変】

図のような直流回路において、抵抗3Ωの端子間の電圧が1.8Vであった。
このとき、電源電圧E[V]の値を求めよ。
【解答】
- 「直流ブリッジの平衡条件
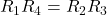 」を満たしているので、12[Ω]の抵抗には電流が流れないため、無視して合成抵抗を求めることができる。
」を満たしているので、12[Ω]の抵抗には電流が流れないため、無視して合成抵抗を求めることができる。
![]() [Ω]
[Ω]
- 「分圧の法則」「分流の法則」より、以下のとおり電源電圧E[V]が求まる。
![]()
![]() [V]
[V]

【電験3種】理論分野の例題・過去問解説と攻略法
電験3種・理論分野の試験対策・問題集についてをまとめました。
コメント