【オペアンプ】微分回路の原理・計算式・例題

オペアンプを用いた微分回路（CR）の原理や計算式、例題について紹介します。

【オペアンプ】微分回路の動作

オペアンプを用いた最も単純な微分回路は以下の通りです。

上記の回路の入力電圧を $V_o$ とするとき、出力電圧 $V_i$ は

(1) $\begin{eqnarray*} V_o=-CR\frac{dV_i}{dt} \end{eqnarray*}$

となります。
この式からもわかるとおり、入力電圧 $V_i$ が時間微分された形で出力電圧 $V_o$ を得ることが出来ます。

先程の計算式の導出を行います。

負帰還回路なので、イマジナリーショートとなり、オペアンプの入力端子(+と-両方)が0{V}になります。
また理想状態では、入力端子間の抵抗値が無限大となるため入力端子へは電流が流れません。

(2) $\begin{eqnarray*} V_+=V_-=0\\ I_+=I_-=0 \end{eqnarray*}$

【イマジナリーショート】
上記の回路は、出力から反転入力(-)に負帰還があります。
このとき、オペアンプの反転入力端子(-)と非反転入力端子(+)が仮想的に短絡状態となり、電位差が0[V]となります。
これをイマジナリーショートと言います。

よって、抵抗Rを流れる電流とコンデンサCを流れる電流は等しくなります。

コンデンサに蓄えられた電荷を $q$ 、コンデンサ及び抵抗を通過して出力端子に向かう電流を $i$ とすると、キルヒホッフの第二法則より

(3) $\begin{eqnarray*} V_i-\frac{q}{C}=0\\ 0-Ri=V_o \end{eqnarray*}$

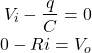
となります。ここで電流と電荷の関係式（ $i=dq/dt$ ）より

(4) $\begin{eqnarray*} V_o=-Ri=-R\frac{dq}{dt}=-CR\frac{dV_i}{dt} \end{eqnarray*}$

となります。

【問題文】
入力電圧に以下のような正弦波交流電圧を加えるとする。

(5) $\begin{eqnarray*} V_i=sinwt \end{eqnarray*}$

このとき、入力電圧 $V_i$ の周波数を2倍にしたとき、出力電圧は何倍になるか。

【解答例】
出力電圧 $V_o$ は

(6) $\begin{eqnarray*} V_o=-CR\frac{dV_i}{dt}=-CRwcoswt \end{eqnarray*}$

となります。
周波数を2倍にすると、各周波数も2倍になります。（w=2πfより）
よって、上式より出力電圧 $V_o$ も2倍となります。

匿名より:

Vi＝sinωtの時の出力電圧の答えにViが入っているのでしょうか。
sinωtをtについて微分するだけなのでωcosωtとなり、それが-CRにかかるため出力電圧Voは
Vo＝-CRωcosωt
となるのではないでしょうか。