交流電圧の正弦波の「実効値」「平均値」の計算式・導出方法についてまとめました。
【交流回路】実効値・平均値の違い
交流電圧における「実効値」「平均値」の定義は次の通りです。
| 値 | 説明 |
|---|---|
| 最大値 |
交流電圧の瞬時値の最大値です。瞬時値とは、任意の時間(瞬間)における値です。 |
| 平均値 |
交流電圧の瞬時値の「絶対値」を1周期 |
| 実効値 |
交流を抵抗に流したときに消費される電力が平均値をとる瞬間の値(交流の大きさは実効値で表すのが基本) |
瞬時値の最大値![]() がわかれば交流電圧(正弦波)の「実効値」「平均値」は次の計算式で求まります。
がわかれば交流電圧(正弦波)の「実効値」「平均値」は次の計算式で求まります。
| 波形の種類 | 実効値 | 平均値 |
|---|---|---|
| 直流 | ||
| 正弦波 |
例
単相2線100V(一般的な家庭用コンセント)の交流電圧は、実効値(公称電圧)が100Vとなります。
最大電圧は√2×100=141.4Vとなります。
平均値は(実効値)x π/2 = 90Vくらいです。
例
3相3線200Vの線間交流電圧は、実効値(公称電圧)が200Vとなります。
最大電圧は√2×200=282.8Vとなります。
相電圧(対地電圧)はフェザー図(Phasor diagram) を用いると
200V ×sin60°×(2/3)=200/√3 V≒115.5 Vとなります。

【補足】平均値の計算式の導出
平均値![]() とは、交流電圧の瞬時値の「絶対値」を1周期
とは、交流電圧の瞬時値の「絶対値」を1周期![]() で平均した値です。
で平均した値です。
そのため、以下の計算式により導出できます。
(1) ![]()
【補足】実効値の計算式の導出
実効値![]() とは、直流換算した場合に直流と同じ電力をもつ交流の大きさ(振幅値)です。
とは、直流換算した場合に直流と同じ電力をもつ交流の大きさ(振幅値)です。
交流電圧を抵抗負荷に加えた場合と、ある直流電圧を加えた場合とで交流電圧の1周期における平均電力が等しくなるときに、この交流電圧は先の直流電圧と同じ値の実効値をもつと定義されます。
つまり、「交流の公称電圧(V) = 実効値」ですが、「直流100Vの時と同じ仕事をする交流の電圧 = 実効値100V」という条件がついて定義されます。
単に100Vと書くと、直流電圧100Vなのか、交流100Vなのか分からないことがあります。
このように、直流と交流をはっきりさせるために「rms」をつけて書くことがあります。
例えば「100V rms」は実効値100V(交流100V)となります。つまり100Vrmsを作るには、振幅の最大値が141.4Vの交流電圧が必要です。
計算式
実効値![]() は以下の計算式により導出できます。
は以下の計算式により導出できます。
(2) 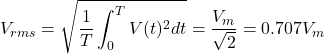
![]() :交流電圧の振幅最大値
:交流電圧の振幅最大値

コメント