電験3種・理論で出題される抵抗率と導電率の計算式と違いについて解説します。
導体の電気抵抗と温度の関係式
- 導体の電気抵抗R[Ω]は以下の式で計算できます。
![]()
- 係数
- ρ 抵抗率[Ω・m]
- ρ’ 抵抗率[Ω・
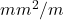 ]
] - A 断面積[
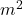 ]
] - l 長さ[
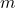 ]
] - d 直径[
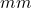 ]
]
- 導体の温度T[℃]及びそのときの抵抗
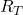 [Ω]の関係は以下の式で表されます。
[Ω]の関係は以下の式で表されます。
![]()
- 係数
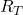 温度T[℃]における抵抗値[Ω]
温度T[℃]における抵抗値[Ω]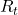 温度t[℃]における抵抗値[Ω]
温度t[℃]における抵抗値[Ω]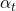 温度t[℃]における抵抗値[Ω]
温度t[℃]における抵抗値[Ω]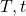 温度[℃]
温度[℃]
- R20を20°Cの抵抗値とすると、T℃のときの抵抗値RT次のようになります。
![]()
- 抵抗温度係数α[1/℃]は以下の式で計算できます。
![]()
- 係数
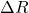 ある温度より1[℃]上昇した場合の抵抗増加分[Ω/℃]
ある温度より1[℃]上昇した場合の抵抗増加分[Ω/℃]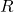 ある温度の抵抗値[Ω]
ある温度の抵抗値[Ω]
- 抵抗温度係数は、温度が高くなるほど大きくなる性質があり、金属導体の場合-20°~+200°Cでは 1°C上昇するごとに次のように増加します。
![]()
- 0℃の銅の抵抗温度係数は0.004264なので銅線の抵抗温度係数αt[1/℃]は以下の式で計算できます。
![]()
- 234.5は、0℃の銅の抵抗温度係数が0.004264なので「1/0.00426≒234.5」からきています。
-
【例題1】銅線コイルの温度上昇時の抵抗値
20〔℃〕のとき、銅線コイルの抵抗値は0.64〔Ω〕であった。
温度が85[℃]のときの抵抗値はいくらになるか。
![]()
関連リンク

【電験3種】理論分野の例題・過去問解説と攻略法
電験3種・理論分野の試験対策・問題集についてをまとめました。

【電験3種】理論分野の例題・過去問解説と攻略法
電験3種・理論分野の試験対策・問題集についてをまとめました。
コメント