【電験3種】法規分野「力率改善」の計算問題・例題

電験3種における法規分野「力率改善」の計算問題・例題のポイントをまとめました。 [latexpage]

【例題】進相コンデンサ設備の容量と力率改善の関係

以下のような三相3線式の高圧電路(線間電圧6600V、無効電力で電圧変動しないと仮定)に三相負荷(300kW、遅れ力率 0.5)の三相負荷が接続されている。この三相負荷と並列に進相コンデンサ設備(直列リアクトル付三相コンデンサ)を接続して力率改善を行うことを考える。直列リアクトルSRのリアクタンスL [Ω] は、三相コンデンサSCのリアクタンスC [Ω] の5％とする。

①三相コンデンサSCの端子電圧[V]を計算せよ。

【解答】三相コンデンサScの端子電圧Vcは、線間電圧Vと分圧の法則より以下のとおりとなる。

\begin{eqnarray} V_C=\frac{-jX_c}{jX_L-jX_C}V \end{eqnarray}

ここで、XLはXcの6%なので以下のとおりとなる。

\begin{eqnarray} V_C=\frac{-jX_c}{0.06jX_C-jX_C}V\\ =\frac{-j}{0.06j-j}V\\ =\frac{-j}{-0.94j}6600\\ =1.064 \cdot 6600\\ =7022 \end{eqnarray}

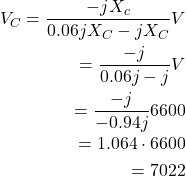
よって、答えは約7022V

②力率を遅れ0.6から遅れ0.8に改善したいとき、三相コンデンサSCに必要な容量 [kvar]を求めよ。

【②解答】

有効電力P・・・抵抗で消費される電力無効電力Q・・・リアクタンスで消費もしくは供給される電力皮相電力S・・・有効電力Pと無効電力Qのベクトル和力率・・・皮相電力のうち有効電力が占める割合

【関係式】 \begin{eqnarray} S=\sqrt{P^2+Q^2}\\ cos\theta=\frac{P}{S}\end{eqnarray}

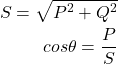
関係式より、無効電力Qを有効電力(負荷で消費される電力)と力率から求められるよう展開していく。 \begin{eqnarray} S^2 = P^2 + Q^2\\ Q^2 = S^2 – P^2 \end{eqnarray}

よって、 \begin{eqnarray} Q = \sqrt{S^2-P^2}\\ =\sqrt{S^2-S^2cos\theta^2}\\ =\sqrt{S^2(1-cos\theta^2)}\\ =S\sqrt{1-cos\theta^2}\\ =\frac{P}{cos\theta}\sqrt{1-cos\theta^2} \end{eqnarray}

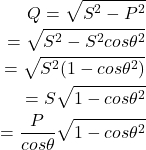
上式より進相コンデンサ設備の接続前の無効電力をQ1、接続後の無効電力をQ2は以下のとおり。

\begin{eqnarray} Q_1=\frac{300}{0.6}\sqrt{1-0.6^2}=400[kvar]\\ Q_2=\frac{300}{0.8}\sqrt{1-0.8^2}=225[kvar] \end{eqnarray}

よって、進相コンデンサによる無効電力の供給容量Qcは以下のとおり。

\begin{eqnarray} Qc=Q_1-Q_2=175[kvar]\end{eqnarray}

ここで進相コンデンサ設備には6%のリアクタンスXLがあるため、三相コンデンサSCの容量Qscは以下のとおり。

\begin{eqnarray} Q_{sc}=\frac{-jX_C}{jX_L-jX_C}Q_C\\ =\frac{-j}{0.06j-j}Q_C\\ =1.064 \cdot Q_C=186[kvar] \end{eqnarray}