電験3種における太陽電池発電設備の架台にかかる荷重の計算例についてをまとめました。
【計算例1】ブレスのない架台の風圧荷重(逆風) + 固定荷重
前提条件(仮定)
| ー | 前提条件(仮定) |
|---|---|
| 1 | 架台正面から見たときの中柱と側柱でモジュールの負担面積は同じ(簡略化のため) ※一般的には、中柱と側柱でモジュールの負担面積が異なり、中柱のほうが負担面積が大きく風圧荷重も大きくなる |
| 2 | 風圧荷重の水平成分は、全て前支柱で負担すると仮定(後支柱は負担が小さいため簡略化) |
パラメータ
| パラメータ | 概要 |
|---|---|
| Wp | 風圧荷重(負圧) |
| Wg | 固定荷重(モジュール全重量+架台重量による荷重) |
| P1 | 前支柱の基礎1箇所に加わる力の鉛直成分 |
| P2 | 後支柱の基礎1箇所に加わる力の鉛直成分 |
| P3 | 前支柱の基礎1箇所に加わる力の水平成分 |
| P4 | 後支柱の基礎1箇所に加わる力の水平成分 |
| n | 柱本数 |
| θ | 傾斜角 |
| H1 | 後支柱の長さ[m] |
| H2 | 前支柱の長さ[m] |
| H3 | 「後支柱の最下部」と「後支柱とブレースの交点」の間隔[m] |
| L | 「パネル受け材の前端」と「パネル受け材の後端」の水平間隔 |
| L1 | 「パネル受け材の前端」と「前支柱」の水平間隔 |
| L2 | 「前支柱」と「後支柱」の水平間隔[m] |
| L3 | 「後支柱」と「パネル受け材の後端」の水平間隔 |
| α1 | 前支柱の負担割合 |
| α2 | 後支柱の負担割合 |
| β | 前支柱(もしくは後支柱)全体のうち、柱1本の負担割合 ※仮定のとおり、中柱と側柱でモジュールの負担面積は同じとすると「n/2」。例えば架台の柱本数n=8ならば8/2=4となる。この4は前支柱、後支柱それぞれの全本数と一致する。つまり、単純に前支柱(もしくは後支柱)の本数で割っている。 |
基礎の荷重計算
(1) 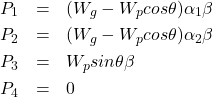
ここで、仮定2より、P4は0となる。また
(2) 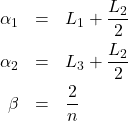
【計算例2】ブレスが前支柱に接続する架台の風圧荷重(逆風) + 固定荷重
前提条件(仮定)
| ー | 前提条件(仮定) |
|---|---|
| 1 | 架台正面から見たときの中柱と側柱でモジュールの負担面積は同じ(簡略化のため) ※一般的には、中柱と側柱でモジュールの負担面積が異なり、中柱のほうが負担面積が大きく風圧荷重も大きくなる |
| 2 | 風圧荷重の水平成分は、ブレスと縦梁の交点を境目として、それより左側で生じる水平力は前支柱、右側で生じる水平力はブレスで負担すると仮定 |
| 3 | 固定荷重と風圧荷重の鉛直成分は、斜材で負担しないと仮定(前支柱と接続されており、負担は小さいため簡略化) |
パラメータ
| パラメータ | 概要 |
|---|---|
| Wp | 風圧荷重(負圧) |
| Wg | 固定荷重(モジュール全重量+架台重量による荷重) |
| P1 | 前支柱の基礎1箇所に加わる力の鉛直成分 |
| P2 | 後支柱の基礎1箇所に加わる力の鉛直成分 |
| P3 | 前支柱の基礎1箇所に加わる力の水平成分 |
| P4 | 後支柱の基礎1箇所に加わる力の水平成分 |
| n | 柱本数 |
| θ | 傾斜角 |
| H1 | 後支柱の長さ[m] |
| H2 | 前支柱の長さ[m] |
| H3 | 「後支柱の最下部」と「後支柱とブレースの交点」の間隔[m] |
| L | 「パネル受け材の前端」と「パネル受け材の後端」の水平間隔 |
| L1 | 「パネル受け材の前端」と「前支柱」の水平間隔 |
| L2 | 「前支柱」と「後支柱」の水平間隔[m] |
| L3 | 「後支柱」と「パネル受け材の後端」の水平間隔 |
| α1 | 前支柱の負担割合 |
| α2 | 後支柱の負担割合 |
| β | 前支柱(もしくは後支柱)全体のうち、柱1本の負担割合 ※仮定のとおり、中柱と側柱でモジュールの負担面積は同じとすると「n/2」。例えば架台の柱本数n=8ならば8/2=4となる。この4は前支柱、後支柱それぞれの全本数と一致する。つまり、単純に前支柱(もしくは後支柱)の本数で割っている。 |
| γ1 | 水平力に対する前支柱の負担割合(仮定2より、ブレスと縦梁の交点を境目として、それより左側で生じる水平力は前支柱が負担するため、「L1/L」となる) |
| γ2 | 水平力に対する後支柱の負担割合(仮定2より、ブレスと縦梁の交点を境目として、それより右側で生じる水平力は後支柱が負担するため、「(L2+L3)/L」となる) |
| F_1 |
基礎の荷重計算
(3) 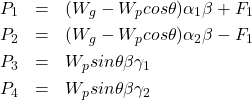
※仮定2より、P4は0
ただし、
(4) 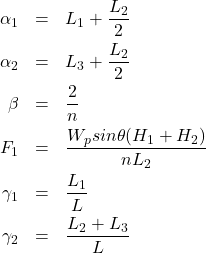

【電験三種】電技28-32条「他の電線、他の工作物等への危険の防止」「支持物の倒壊による危険の防止」の対策
電験三種(法規)における電技28-31条「他の電線、他の工作物等への危険の防止」の攻略ポイントをまとめました。

【電験3種・法規】39条〜41条「技術基準への適合」の出題範囲と攻略ポイント
電験3種の法規「電気事業法」の技術基準への適合の出題範囲とポイントについてまとめました。
コメント